Question

You hear from a friend that you should invest in bonds, and that Pepsi Co should be a solid (safe) investment because everyone drinks Pepsi. After looking up the information, you find the following. Calculate the current price you Pepsi Co bonds would cost today. Assume that the bond is based off of the highlighted portions as seen to the right, and that the YTM is 3.27%

Issue Date: 2/24/2016

Coupon rate: 2.850%

Maturity Date: 2/24/2026

Number of payments per yr: 2

insert the following information:

PV

I/Y

N

PMT

FV

Answer 1

$964.42 approx.

Step-by-step explanation:

Current value of a bond is the present value of it's future stream of coupon payments as well as it's redemption value upon maturity.

Here, coupon rate = 2.850/2 = 1.425% per period

N = no of periods = 10 years × 2 = 20 periods

Face Value = $1000 assumed

Yield to maturity (YTM) = 3.27/2 = 1.635%

Present Value or
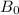`B_(0)` shall be calculated as:

`B_(0) = (C)/((1\ +\ YTM)^(1) ) \ +\ (C)/((1\ +\ YTM)^(2) ) \ +........+\ (C)/((1\ +\ YTM)^(20) ) \ + (RV)/((1\ +\ YTM)^(20) )`

`B_(0) = (14.25)/((1\ +\ .01635)^(1) ) \ +\ (14.25)/((1\ +\ .01635)^(2) ) \ +........+\ (14.25)/((1\ +\ .01635)^(20) ) \ + (1000)/((1\ +\ .01635)^(20) )`

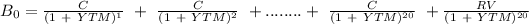
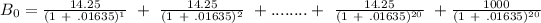
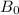`B_(0)` = 16.94 × 14.25 + 722.99 = 241.4280 +722.99

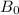`B_(0)` = $ 964.418

Thus, current price of the bond is $964.42 approx.