Question

The diameter of a sphere is 2,160 mm. The diameter of a second sphere is 7,520 mm. Approximately how many times larger is the volume of the second sphere than the volume of the first sphere?

Answer 1

Approximately 42 times larger

Explanation:

The diameter of a sphere is 2,160 mm.

The diameter of a second sphere is 7,520 mm.

To see how many times larger is the diameter of second sphere is than the diameter of the second sphere, we divide to get:

`k = (7520)/(2160)`

`k = 3.481`

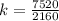
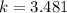
To see how many times larger the volume is, we cube both sides

`{k}^(3) = {3.481}^(3)`

This implies that

`{k}^(3) = 42.181`

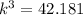
Therefore the volume of the second sphere is approximately 42 times larger