Question

If tangent alpha equals negative StartFraction 21 Over 20 EndFraction ​, 90degreesless thanalphaless than180degrees​, then find the exact value of each of the following. a. sine StartFraction alpha Over 2 EndFraction b. cosine StartFraction alpha Over 2 EndFraction c. tangent StartFraction alpha Over 2 EndFraction

Answer 1

α= 133.6 degrees

(a)Sin(α/2)=0.9191

(b)cos(α/2)=0.3939

(c)Tan(α/2)=2.3332

Explanation:

If Tan α=
`-(21)/(20)`

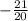
90<α<180

We determine first the value of α in the first quadrant

α=
`Tan^(-1)(21)/(20)`

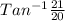
=46.4

Since 90<α<180

α=180-46.4=133.6 degrees

(a)Sin(α/2)=Sin(133.6/2)=Sin 66.8 =0.9191

(b)cos(α/2)=cos(133.6/2)=cos 66.8 =0.3939

(c)Tan(α/2)=Tan(133.6/2)=Tan 66.8 =2.3332