Given:-
- ABC is a triangle.
 BAC = 40°.
BAC = 40°.
 ABC = 70°.
ABC = 70°.
To Find:-
- Measure of
 ACD.
ACD.
Solution:-
➾Firstly, we will find the measure of
 ACB.
ACB.
We know that,
Sum of all interior angles of a triangle = 180°.

 BAC +
BAC +
 ABC +
ABC +
 ACB = 180°
ACB = 180°
 40°+70°+
40°+70°+
 ACB = 180°
ACB = 180°
 110°+
110°+
 ACB = 180°
ACB = 180°

 ACB = 180°-110°
ACB = 180°-110°

 ACB = 70°
ACB = 70°
So, the measure of
 ACB = 70°.
ACB = 70°.
➾ Side BC of the triangle is extended till D. So, we have to find the measure of
 ACD.
ACD.
As we know that,
Sum of any two or more angles that lie on a straight line = 180°.
So,
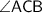 +
+
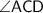 = 180°
= 180°
 70° +
70° +
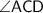 = 180°
= 180°

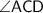 = 180°-70°
= 180°-70°

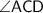 = 110°.
= 110°.
Therefore, measure of
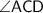 = 110°.
= 110°.
____________________________
Hope it helps you:)