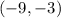Question

What’s the answer cause I need it bad

Answer 1

Answer:
`(-9,-3)`

Explanation:

Given the following system of equations:

`\left \{ {{2x=-78-20y} \atop {-x=-51-20y}} \right.`

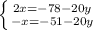
In order to solve the System of equations, you can use the Substitution method. The steps are:

1. You can solve for "x" from the second equation:

`-x=-51-20y\\\\x=51+20y`

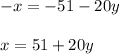
2. Substitute the equation obtained into the first original equation:

`2x=-78-20y\\\\2(51+20y)=-78-20y`

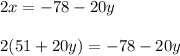
3. Now you must solve for "y":

`102+40y=-78-20y\\\\40y+20y=-78-102\\\\60y=-180\\\\y=(-180)/(60)\\\\y=-3`

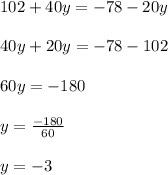
4. Substitute the value of "y" into the equation
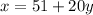`x=51+20y` and evaluate:

`x=51+20(-3)\\\\x=51-60\\\\x=-9`

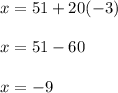
Then, the solution is:

`(-9,-3)`