Question

What are the coordinates of the vertex of the function f(x) = x2 - 12x + 5?

(6,31)
(-6, 31)
(6,-31)
(-6, -31)

Answer 1

C

Explanation:

Just took the test

Answer 2

The vertex is the point (6,-31)

Explanation:

we have

`f(x)=x^2-12x+5`

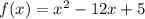
This is a vertical parabola open upward

The vertex represent a minimum

Convert to vertex form

Complete the square

`f(x)=(x^2-12x+6^2)+5-6^2`

`f(x)=(x^2-12x+36)-31`

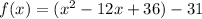
Rewrite as perfect squares

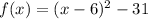`f(x)=(x-6)^2-31` -----> equation in vertex form

therefore

The vertex is the point (6,-31)