Question

Need help on problem 40 part b for integrating in respect to y! Thanks!

Answer 1

Answer:
`\bold{(a)\quad (32)/(3)\qquad (b)\quad (32)/(3)}`

Explanation:

(a) First, find the x-coordinates where the two equations cross

y = -1 and y = 3 - x²

-1 = 3 - x²

-4 = -x²

4 = x²

± 2 = x → These are the upper and lower limits of your integral

Then subtract the two equations and integrate with upper bound of x = 2 and lower bound of x = -2

`\int_(-2)^(+2)[(3-x^2)-(-1)]dx\\\\\\=\int_(-2)^2(4-x^2)dx\\\\\\=4x-(x^3)/(3)\bigg|_(-2)^(+2)\\\\\\=\bigg(8-(8)/(3)\bigg)-\bigg(-8+(8)/(3)\bigg)\\\\\\=\large\boxed{(32)/(3)}`

(b) We know the upper and lower bounds of the y-axis as y = 3 and y = -1

Next, find the equation that we need to integrate by solving for x.

y = 3 - x²

x² + y = 3

x² = 3 - y

x
`=\pm√(3-y)\\`

`\rightarrow \qquad x=√(3-y)\quad and \quad x=-√(3-y)`

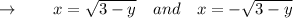
Now, subtract the two equations and integrate with upper bound of y = 3 and lower bound of y = -1

`\int_(-1)^(+3)[(√(3-y))-(-√(3-y))]dy\\\\\\=\int_(-1)^(+3)(2√(3-y))dy\\\\\\=(-4√((3-y)^3))/(3)\bigg|_(-1)^(+3)\\\\\\=\bigg(0\bigg)-\bigg(-(32)/(3)\bigg)\\\\\\=\large\boxed{(32)/(3)}`