Answer:
0.6517
Explanation:
Given that in a certain game of chance, your chances of winning are 0.3.
We know that each game is independent of the other and hence probability of winning any game = 0.3 (constant)
Also there are only two outcomes
Let X be the number of games you win when you play 4 times
Then X is binomial with p = 0.3 and n =4
Required probability
= Probability that you win at most once
=
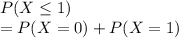
We have as per binomial theorem
P(X=r) =
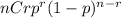
Using the above the required prob
= 0.6517