Answer:

For this case we know this:
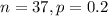
We can find the standard error like this:

So then our random variable can be described as:
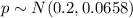
Let's suppose that the question on this case is find the probability that the population proportion would be higher than 0.4:
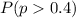
We can use the z score given by:
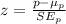
And using this we got this:
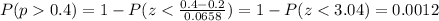
And we can find this probability using the Ti 84 on this way:
2nd> VARS> DISTR > normalcdf
And the code that we need to use for this case would be:
1-normalcdf(-1000, 3.04; 0;1)
Or equivalently we can use:
1-normalcdf(-1000, 0.4; 0.2;0.0658)
Explanation:
We need to check if we can use the normal approximation:
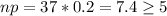
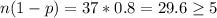
We assume independence on each event and a random sampling method so we can conclude that we can use the normal approximation and then ,the population proportion have the following distribution :

For this case we know this:
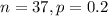
We can find the standard error like this:

So then our random variable can be described as:
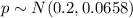
Let's suppose that the question on this case is find the probability that the population proportion would be higher than 0.4:
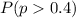
We can use the z score given by:
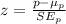
And using this we got this:
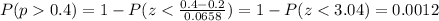
And we can find this probability using the Ti 84 on this way:
2nd> VARS> DISTR > normalcdf
And the code that we need to use for this case would be:
1-normalcdf(-1000, 3.04; 0;1)
Or equivalently we can use:
1-normalcdf(-1000, 0.4; 0.2;0.0658)