Question

A pizza place recently hired additional drivers and as a result now claims that its average delivery time for orders is under 44 minutes. A sample of 39 customer deliveries was​ examined, and the average delivery time was found to be 40.5 minutes.​ Historically, the standard deviation for delivery time is 11.3 minutes. Using alphaequals0.05​, complete parts a and b below. a. Does this sample provide enough evidence to support the delivery time claim made by the pizza​ place? Determine the null and alternative hypotheses. Upper H 0​: mu greater than or equals 44 Upper H 1​: mu less than 44 The​ z-test statistic is negative 1.93. ​(Round to two decimal places as​ needed.) The critical​ z-score(s) is(are) 1.64 comma negative 1.64. ​(Round to two decimal places as needed. Use a comma to separate answers as​ needed.)

Answer 1

Yes, this sample provide enough evidence to support the delivery time claim made by the pizza​ place.

Explanation:

We are given that a pizza place recently hired additional drivers and as a result now claims that its average delivery time for orders is under 44 minutes.

A sample of 39 customer deliveries was​ examined, and the average delivery time was found to be 40.5 minutes.​ Historically, the standard deviation for delivery time is 11.3 minutes.

From this, X bar = 40.5 ,
`\sigma` = 11.3 ,
`\mu` = 44 and sample, n = 39

Null Hypothesis,
`H_0` :
`\mu` >= 44

Alternate Hypothesis,
`H_1` :
`\mu` < 44

The test statistics used here will be;

T.S. =
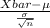`(Xbar-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

So, Test statistics =
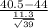`(40.5-44)/((11.3)/(√(39) ) )` = -1.93

Now, at 5% significance level the z score table gives critical value of -1.6449 as it is one-tail test.

Since our test statistics is less than the critical value as -1.93 < -1.6449, so we have sufficient evidence to reject null hypothesis and conclude that the average delivery time for orders is under 44 minutes.