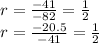Answer:
1/2
Step-by-step explanation:
Given a certain sequence of number,
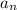
The common ratio of the sequence is rhe ratio between two consecutive numbers of the sequence, namely:
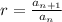
In this problem, the sequence contains the numbers:
-164, -82, -41, -20.5
We can calculate the common ratio by taking the 1st and 2nd number; we have:
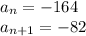
Therefore, the common ratio is:
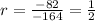
And we can easily verify that this ratio is valid also for the other numbers in the sequence: