Question

Although cities encourage carpooling to reduce traffic congestion, most vehicles carry only one person. For example, 64% of vehicles on the roads are occupied by just the driver. (Round your answers to four decimal places.)A) If you choose 10 vehicles at random, what is the probability that more than half (that is, 6 or more) carry just one person?

B) If you choose 92 vehicles at random, what is the probability that more than half (that is, 47 or more) carry just one person? (Use the normal approximation.)

Answer 1

a) 0.7291 is the probability that more than half out of 10 vehicles carry just 1 person.

b) 0.996 is the probability that more than half of the vehicles carry just one person.

Explanation:

We are given the following information:

A) Binomial distribution

We treat vehicle on road with one passenger as a success.

P(success) = 64% = 0.64

Then the number of vehicles follows a binomial distribution, where

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

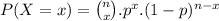
where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 10

We have to evaluate:

`P(x \geq 6) = P(x =6) +...+ P(x = 10) \\= \binom{10}{6}(0.64)^6(1-0.64)^4 +...+ \binom{10}{10}(0.64)^(10)(1-0.79)^0\\=0.7291`

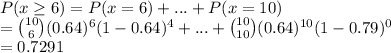
0.7291 is the probability that more than half out of 10 vehicles carry just 1 person.

B) By normal approximation

Sample size, n = 92

p = 0.64

`\mu = np = 92(0.64) = 58.88`

`\sigma = √(np(1-p)) = √(92(0.64)(1-0.64)) = 4.60`

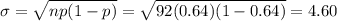
We have to evaluate the probability that more than 47 cars carry just one person.

`P(x \geq 47)`

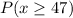
After continuity correction, we will evaluate

`P( x \geq 46.5) = P( z > \displaystyle(46.5 - 58.88)/(4.60)) = P(z > -2.6913)`

`= 1 - P(z \leq -2.6913)`

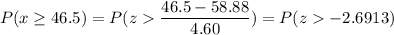
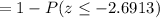
Calculation the value from standard normal z table, we have,

`P(x > 46.5) = 1 - 0.004 = 0.996 = 99.6\%`

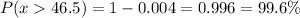
0.996 is the probability that more than half out of 92 vehicles carry just one person.