Answer:
It would take 90 hours to fill the pool.
Step-by-step explanation:
There is a mistake in the question so it is corrected below:
An inlet pipe on a swimming pool can be used to fill the pool in 40 hours. The drain pipe can be used to empty the pool in 45 hours. If the pool is 1/4 filled and then the inlet pipe and drain pipe are opened, how many more hours would it take to fill the pool?
Now, to find the hours would it take to fill the 1/4 pool.
Let the hours it take to fill the
 pool be
pool be
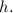
A swimming pool can be used to fill the pool in 40 hours.
So, the rate of filling the pool =
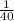 .
.
As, given the drain pipe can be used to empty the pool in 45 hours.
Thus, the rate of draining the pool =
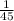 .
.
According to question:
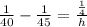

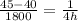
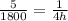
Using cross multiplication:
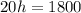
Dividing both sides by 20 we get:
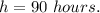
Therefore, it would take 90 hours to fill the pool.