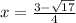Question

If the quadratic formula is used to solve 2x2 - 3x - 1 = 0, what are the solutions?

Answer 1

The solutions are
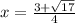`x=(3+√(17))/(4)` and
`x=(3-√(17))/(4)`

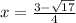
Step-by-step explanation:

The given equation is
`2 x^(2)-3 x-1=0`

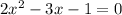
The solution can be determined by using the quadratic formula.

To determine the solution of the given equation, let us solve using the quadratic formula.

The quadratic formula is given by

`x=\frac{-b\pm\sqrt{b^(2)-4 a c}}{2 a}`

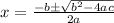
where
`a=2, b=-3, c=-1`

Substituting these values in the quadratic formula, we have,

`x=\frac{-(-3) \pm \sqrt{(-3)^(2)-4 \cdot 2(-1)}}{2 \cdot 2}`

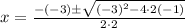
Simplifying, we get,

`x=(3 \pm √(9+8))/(4)`

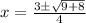
Adding the terms within the square root, we get,

`x=(3 \pm √(17))/(4)`

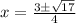
Thus, we have,

`x=(3+√(17))/(4)` ,
`x=(3-√(17))/(4)`

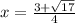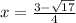
Thus, the solutions of the quadratic equation are
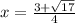`x=(3+√(17))/(4)` and
`x=(3-√(17))/(4)`