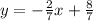Question

What is the inverse relation of thr function f(x) = -7/2x+4

Answer 1

The inverse of the function is
`y=-(2)/(7) x+(8)/(7)`

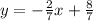
Step-by-step explanation:

The given function is
`f(x)=-(7)/(2) x+4`

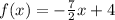
To determine the inverse of a function, we need to interchange the variables and solve for y.

Let us interchange the variables x and y

Thus, we have,

`x=-(7)/(2) y+4`

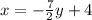
Now, we shall solve for y

Subtracting both sides of the equation by 4, we get,

`x-4=-(7)/(2) y`

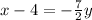
Multiplying both sides of the equation by
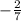`-(2)/(7)`, we get,

`-(2)/(7) (x-4)= y`

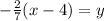
Switch sides, we have,

`y=-(2)/(7) (x-4)`

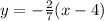
Multiplying the terms within the bracket, we have,

`y=-(2)/(7) x+(8)/(7)`

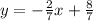
Thus, the inverse of the function is
`y=-(2)/(7) x+(8)/(7)`