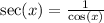Question

Which inequality would result in the shaded solution on the unit circle to the right?

Answer 1

0 ≤ sin x < 1/2.

Step-by-step explanation:

sin π6 = 1/2

sin 5π/6 = 1/2

sin 0 and sin 180 = 0

The dotted line indicates that the value of the sine is less than 1/2 and the solid line indicates that value is greater or equal to zero.

So the inequality is 0 ≤ sin x < 1/2

Answer 2

Answer: Choice B

Step-by-step explanation:

Cosine is positive in quadrants I and IV, but quadrant IV isn't shaded in so we can rule out choice A.

Sine is positive in quadrants I and II. So far it looks like choice B could work. In fact, it's the answer because sin(pi/6) = 1/2 and sin(5pi/6) = 1/2. So if 0 ≤ sin(x) < 1/2, then we'd shade the region between theta = 0 and theta = pi/6; as well as the region from theta = 5pi/6 to theta = pi.

Choice C is ruled out because tangent is positive in quadrants I and III, but quadrant III isn't shaded.

Choice D is ruled out for similar reasoning as choice A. Recall that
`\sec(x) = (1)/(\cos(x))`