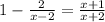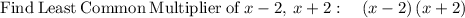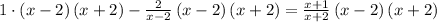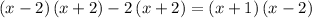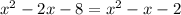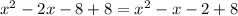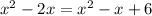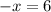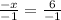Question

asked Jan 21, 2021 161k views

1 Answer

AareP · Answer 1 · 2021-01-27T19:41:26+0000

Part a)

Given the simplified expression

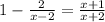
1-(2)/(x-2)=(x+1)/(x+2)

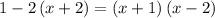
$1-2\left(x+2\right)=\left(x+1\right)\left(x-2\right)$

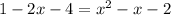
$\:1-2x-4=x^2-x-2$

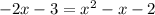
$-2x-3=x^2-x-2\:\:$

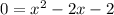
$0=x^2-2x-2\:\:$

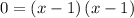
$0=\left(x-1\right)\left(x-1\right)$

x=1

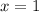
Identifying the Main Error

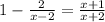
1-(2)/(x-2)=(x+1)/(x+2)

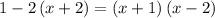$1-2\left(x+2\right)=\left(x+1\right)\left(x-2\right)$ ← ERROR Starts here

Here is the Explanation of the Error

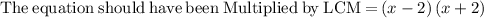$\mathrm{The\:equation\:should\:have\:been\:Multiplied\:by\:LCM=}\left(x-2\right)\left(x+2\right)$ . In your case you wrongly multiply the equation.

CORRECTION

HERE IS HOW YOU SHOULD HAVE MULTIPLIED BY LCM = (x-2)(x+2):

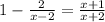
1-(2)/(x-2)=(x+1)/(x+2)

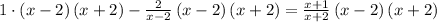
$1\cdot \left(x-2\right)\left(x+2\right)-(2)/(x-2)\left(x-2\right)\left(x+2\right)=(x+1)/(x+2)\left(x-2\right)\left(x+2\right)$

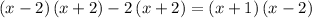
$\left(x-2\right)\left(x+2\right)-2\left(x+2\right)=\left(x+1\right)\left(x-2\right)$

Here is the complete correction of the error.

Considering the expression

1-(2)/(x-2)=(x+1)/(x+2)

$\mathrm{Find\:Least\:Common\:Multiplier\:of\:}x-2,\:x+2:\quad \left(x-2\right)\left(x+2\right)$

$1\cdot \left(x-2\right)\left(x+2\right)-(2)/(x-2)\left(x-2\right)\left(x+2\right)=(x+1)/(x+2)\left(x-2\right)\left(x+2\right)$

$\left(x-2\right)\left(x+2\right)-2\left(x+2\right)=\left(x+1\right)\left(x-2\right)$

x^2-2x-8=x^2-x-2

x^2-2x-8+8=x^2-x-2+8

x^2-2x=x^2-x+6

-x=6

(-x)/(-1)=(6)/(-1)

x=-6