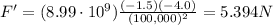Question

(a) Determine the change in electric potential energy of a system of two charged objects when a -1.5-C charged object and a -4.0-C charged object move from an initial separation of 500 km to a final separation of 100 km. (b) What other quantities can you calculate using this information?

Answer 1

a)
`4.32\cdot 10^5 J`

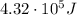
b) Electric force

Step-by-step explanation:

a)

The electric potential energy of a system of charge is given by

`U=k(q_1 q_2)/(r)`

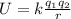
where:

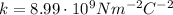`k=8.99\cdot 10^9 Nm^(-2)C^(-2)` is the Coulomb's constant

`q_1, q_2` are the two charges

r is the separation between the two charges

In this problem, we have:

`q_1=-1.5 C` (1st charge)

`q_2=-4.0 C` (2nd charge)

The initial distance is

`r=500 km= 500,000m`

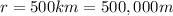
So the initial potential energy is

`U=(8.99\cdot 10^9)((-1.5)(-4.0))/((500,000))=1.08\cdot 10^5 J`

Later, the distance is decreased to

`r'=100 km = 100,000 m`

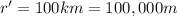
So the final potential energy is

`U=(8.99\cdot 10^9)((-1.5)(-4.0))/((100,000))=5.4\cdot 10^5 J`

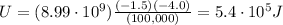
Therefore, the change in electric potential energy is:

`\Delta U=U'-U=5.4\cdot 10^5 - 1.08\cdot 10^5=4.32\cdot 10^5 J`

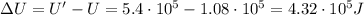
b)

There are several other quantities that we can calculate for this system of charges; for example, we can calculate the magnitude of the electric force between them.

The electric force between two charges is given by

`F=k(q_1 q_2)/(r^2)`

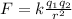
where:

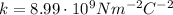`k=8.99\cdot 10^9 Nm^(-2)C^(-2)` is the Coulomb's constant

`q_1, q_2` are the two charges

r is the separation between the two charges

So at the beginning, when the distance is

`r=500,000 m`

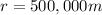
The force is

`F=(8.99\cdot 10^9)((-1.5)(-4.0))/((500,000)^2)=0.216 N`

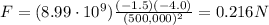
While later, when the distance is

`r'=100,000 m`

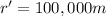
The force is

`F'=(8.99\cdot 10^9)((-1.5)(-4.0))/((100,000)^2)=5.394 N`