Answer:
a) H0:
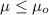
H1:
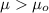
n = 13 represent the sample size
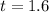 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
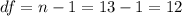
We can calculathe the p value with this formula:
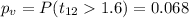
Since
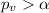 we fail to reject the null hypothesis on this case at 5% of significance.
we fail to reject the null hypothesis on this case at 5% of significance.
b) H0:
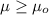
H1:
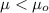
n = 13 represent the sample size
 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
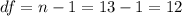
We can calculathe the p value with this formula:
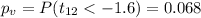
Since
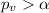 we fail to reject the null hypothesis on this case at 5% of significance.
we fail to reject the null hypothesis on this case at 5% of significance.
c) H0:
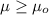
H1:
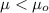
n = 25 represent the sample size
 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
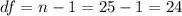
We can calculathe the p value with this formula:
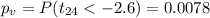
Since
 we can reject the null hypothesis on this case at 1% of significance.
we can reject the null hypothesis on this case at 1% of significance.
Explanation:
Part a
For this case we assume that we are testing the following system of hypothesis
H0:
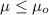
H1:
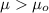
n = 13 represent the sample size
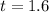 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
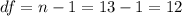
We can calculathe the p value with this formula:
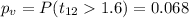
Since
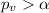 we fail to reject the null hypothesis on this case at 5% of significance.
we fail to reject the null hypothesis on this case at 5% of significance.
Part b
For this case we assume that we are testing the following system of hypothesis
H0:
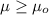
H1:
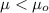
n = 13 represent the sample size
 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
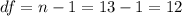
We can calculathe the p value with this formula:
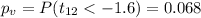
Since
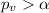 we fail to reject the null hypothesis on this case at 5% of significance.
we fail to reject the null hypothesis on this case at 5% of significance.
Part c
For this case we assume that we are testing the following system of hypothesis
H0:
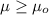
H1:
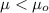
n = 25 represent the sample size
 represent the calculated statistic
represent the calculated statistic
The degrees of freedom are given by:
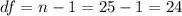
We can calculathe the p value with this formula:
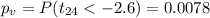
Since
 we can reject the null hypothesis on this case at 1% of significance.
we can reject the null hypothesis on this case at 1% of significance.