Question

A rigid tank contains 0.66 mol of oxygen (O2). Find the mass of oxygen that must be withdrawn from the tank to lower the pressure of the gas from 43 atm to 17 atm. Assume that the volume of the tank and the temperature of the oxygen are constant during this operation. Answer in units of g.

Answer 1

12.8 g of
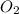`O_(2)` must be withdrawn from tank

Step-by-step explanation:

Let's assume
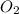`O_(2)` gas inside tank behaves ideally.

According to ideal gas equation-
`PV=nRT`

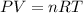
where P is pressure of
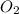`O_(2)`, V is volume of
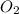`O_(2)`, n is number of moles of
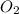`O_(2)`, R is gas constant and T is temperature in kelvin scale.

We can also write,
`(V)/(RT)=(n)/(P)`

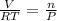
Here V, T and R are constants.

So,
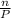`(n)/(P)` ratio will also be constant before and after removal of
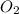`O_(2)` from tank

Hence,
`(n_(before))/(P_(before))=(n_(after))/(P_(after))`

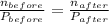
Here,
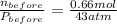`(n_(before))/(P_(before))=(0.66mol)/(43atm)` and
`P_(after)=17atm`

So,
`n_(after)=(n_(before))/(P_(before))* P_(after)=(0.66mol)/(43atm)* 17atm=0.26mol`

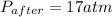
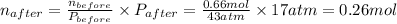
So, moles of
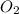`O_(2)` must be withdrawn = (0.66 - 0.26) mol = 0.40 mol

Molar mass of
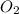`O_(2)` = 32 g/mol

So, mass of
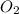`O_(2)` must be withdrawn =
`(32* 0.40)g=12.8g`