Answer:
The equation of given circle with centre C ( 8 , - 10 ) and diameter ( 8√3 ) is x² + y² - 16x + 20y + 116 = 0

Solution:
The standard equation of Circle is given by :
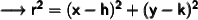
This is the standard form of the equation. Thus if we know the coordinates of center of the circle and it's radius, we can easily find its equation
Here, in this question we are given that the centre C is ( 8 , -10 ) and diameter 8√3.
 h = 8
h = 8
 k = - 10
k = - 10
 r =
r =
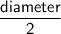
 r =
r =
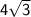

On putting the values in the formula :
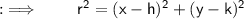
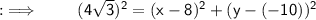
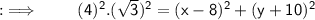
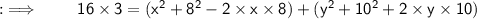

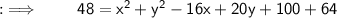

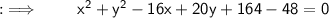

ㅤㅤㅤㅤ~Hence, the required equation of Circle is x² + y² - 10x + 20y + 116 = 0