1 Answer

Ladislas Nalborczyk · Answer 1 · 2021-12-17T12:02:33+0000

Option C

The probability that it will be the winning combination is:

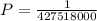
P = (1)/(427518000)

Solution:

The probability is given as:

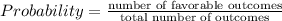
$Probability = \frac{\text{number of favorable outcomes}}{\text{total number of outcomes}}$

Given that,

A state lottery involves the random selection of six different numbers between 1 and 30

There are 30 numbers from 1 to 30

The probability that the first digit of lottery number is same as picked can be calculated as:

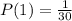
P(1) = (1)/(30)

Since, already we picked 1 digit, now total outcomes = 30 - 1 = 29

The probability that the second digit of lottery number is same as picked can be calculated as:

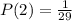
P(2) = (1)/(29)

Similarly, The probability that the all digit of lottery number is same as picked can be calculated as:

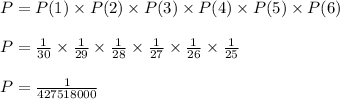
$P = P(1) * P(2) * P(3) * P(4) * P(5) * P(6)\\\\P = (1)/(30) * (1)/(29) * (1)/(28) * (1)/(27) * (1)/(26) * (1)/(25)\\\\P = (1)/(427518000)$

Thus Option C is correct

Please log in or register to add a comment.