Question

For the figures below, assume they are made of semicircles, quarter circles and squares. For each shape, find the area and perimeter. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answer 1

Area of the shaded region
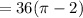`$=36(\pi -2)` square cm

Perimeter of the shaded region
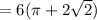`=6 (\pi + 2\sqrt 2)` cm

Solution:

Radius of the quarter of circle = 12 cm

Area of the shaded region = Area of quarter of circle – Area of the triangle

`$=(1)/(4) \pi r^2 - (1)/(2) bh`

`$=(1)/(4) \pi * 12^2 - (1)/(2) * 12 * 12`

`$=36\pi -72`

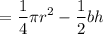
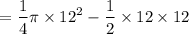
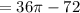
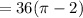`$=36(\pi -2)` square cm.

Area of the shaded region
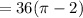`$=36(\pi -2)` square cm

Using Pythagoras theorem,

`AC^2=AB^2+BC^2`

`AC^2=12^2+12^2`

`AC^2=288`

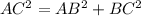
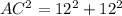
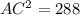
Taking square root on both sides of the equation, we get

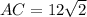`AC= 12\sqrt 2` cm

Perimeter of the quadrant of a circle =
`(1)/(4) * 2\pi r`

`$=(1)/(4) * 2 * \pi * 12`

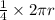
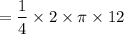
`$=6 \pi` cm

Perimeter of the shaded region =
`6 \pi + 12\sqrt 2` cm

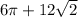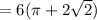`=6 (\pi + 2\sqrt 2)` cm

Hence area of the shaded region
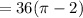`$=36(\pi -2)` square cm

Perimeter of the shaded region
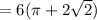`=6 (\pi + 2\sqrt 2)` cm