Answer:
The mass of SbCl₅ in 2.00-L flask = 14.95 g
The mass of SbCl₃ in 2.00-L flask = 11.41 g
The mass of Cl₂ in 2.00-L flask = 3.55 g
Step-by-step explanation:
Equation for the reaction is given as:
SbCl5(g)⇌SbCl3(g)+Cl2(g)
Equilibrium constant
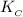 =
=
![([SbCl_3][Cl_2])/([SbCl_5])](https://img.qammunity.org/2021/formulas/chemistry/college/jqg8eyxy7qyl9egc2lht4qerus3qad0n76.png)
Let's calculate their respective number of moles; followed by their molar concentrations.
Since number of moles
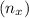 =
=
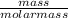
Therefore;
For SbCl₅(g)
mass given =3.85 g
molar mass = 299 g/mol
number of moles of SbCl₅(g) will be:
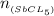 =
=

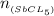 = 0.0128 moles
= 0.0128 moles
For SbCl₃(g);
mass given = 9.14 g
molar mass = 228.13 g/mol
number of moles of SbCl₃(g) will be:
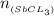 =
=

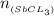 = 0.0400 moles
= 0.0400 moles
For Cl₂(g)
mass given 2.84 g
molar mass = 70.906 g/mol
number of moles of Cl₂(g) will be:
 =
=
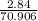
 = 0.0400 moles
= 0.0400 moles
Molar Concentration =
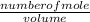
Their respective molar concentration can be calculated as follows:
Molar Concentration for SbCl₅(g)
[SbCl₅(g)] =
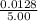
= 0.00256
= 2.56 × 10⁻³ M
Molar Concentration for SbCl₃(g)
[SbCl₃(g)] =
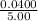
= 0.008
= 8 × 10⁻³ M
Molar Concentration for Cl₂(g)
[Cl₂(g)] =
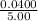
= 0.008
= 8 × 10⁻³ M
Again, we knew our Equilibrium constant
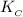 =
=
![([SbCl_3][Cl_2])/([SbCl_5])](https://img.qammunity.org/2021/formulas/chemistry/college/jqg8eyxy7qyl9egc2lht4qerus3qad0n76.png)
∴
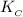 =
=
![([8*10^(-3)][8*10^(-3)])/([2.56*10^(-3)])](https://img.qammunity.org/2021/formulas/chemistry/college/ujfj19z2r39fkzf6i8sbtdi9gbhs6mss0r.png)
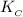 = 0.025
= 0.025
For the equilibrium mixture in 5.00 L flask at 448°C;
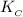 = 0.025
= 0.025
∴ For 2.00 L;
Let (y) M be the concentration of SbCl₅(g), SbCl₃(g) and Cl₂(g)
∴
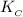 =
=
![([y][y])/([y])](https://img.qammunity.org/2021/formulas/chemistry/college/ms9327wv2nfsrp97jqc3y9es3xem1a1nr5.png)
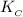 = y
= y
0.0025 = y
∴ For SbCl₅(g), SbCl₃(g) and Cl₂(g) in 2.00-L; their respective Molar Concentration is 0.025 M each.
So, since numbers of moles =
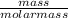
mass = numbers of moles × molar mass
Also, numbers of moles = Molar Concentration × Volume
∴ mass = Molar Concentration × Volume × molar mass
For SbCl₅(g);
mass = 0.025 × 2 × 229g
= 14.95 g
For SbCl₃(g);
mass = 0.025 × 2 × 228.13
= 11.4065 g
≅ 11.41 g
For Cl₂(g):
mass = 0.025 × 2 × 70.906
= 3.5453 g
≅ 3.55 g
∴
The mass of SbCl₅ in 2.00-L flask = 14.95 g
The mass of SbCl₃ in 2.00-L flask = 11.41 g
The mass of Cl₂ in 2.00-L flask = 3.55 g