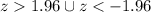Answer:
a) We have that the significance is given by
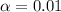 and we know that we have a right tailed test.
and we know that we have a right tailed test.
So for this case we need to look in the normal standard dsitribution a critical value that accumulates 1% of the area on the right and 99% of the area on the left. This value can be founded with the following excel code:
"=NORM.INV(1-0.01,0,1)"
And we got for this case
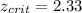
So then the rejection region would be
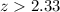
b) We have that the significance is given by
 ,
,
 and we know that we have a two tailed test.
and we know that we have a two tailed test.
So for this case we need to look in the normal standard dsitribution a critical value that accumulates 2.5% of the area on the right and 97.5% of the area on the left. This value can be founded with the following excel code:
"=NORM.INV(1-0.025,0,1)"
And we got for this case

So then the rejection region would be
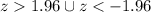
Explanation:
Part a
We have that the significance is given by
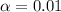 and we know that we have a right tailed test.
and we know that we have a right tailed test.
So for this case we need to look in the normal standard dsitribution a critical value that accumulates 1% of the area on the right and 99% of the area on the left. This value can be founded with the following excel code:
"=NORM.INV(1-0.01,0,1)"
And we got for this case
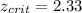
So then the rejection region would be
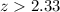
Part b
We have that the significance is given by
 ,
,
 and we know that we have a two tailed test.
and we know that we have a two tailed test.
So for this case we need to look in the normal standard dsitribution a critical value that accumulates 2.5% of the area on the right and 97.5% of the area on the left. This value can be founded with the following excel code:
"=NORM.INV(1-0.025,0,1)"
And we got for this case

So then the rejection region would be