Question

The population of a bacteria in an experiment has been increasing by 80% each day. If there were 25 bacteria at the beginning of the experiment, predict the number of bacteria in 10 days

Answer 1

8926 bacteria

Explanation:

We have been given that the population of a bacteria in an experiment has been increasing by 80% each day. There were 25 bacteria at the beginning of the experiment. We are asked to find the number of bacteria in 10 days.

We will use exponential growth formula to solve our given problem.

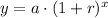`y=a\cdot (1+r)^x`, where,

y = Final amount

a = Initial amount,

r = Growth rate in decimal form,

x = Time.

`80\%=(80)/(100)=0.80`

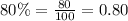
Upon substituting our given values in above formula, we will get:

`P(t)=25(1+0.80)^t`

`P(t)=25(1.80)^t`

To find number of bacteria in 10 days, we will substitute
`t=10` in our formula as:

`P(10)=25(1.80)^(10)`

`P(10)=25(357.0467226624)`

`P(10)=8926.16806656\approx 8926`

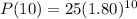
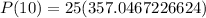
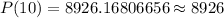
Therefore, there will be approximately 8926 bacteria in 10 days.