Answer:
Ionic radius of the bromide ion is 227.9 pm.
Step-by-step explanation:
Number of atom in FCC unit cell = Z = 4
Density of ammonium bromide =

Edge length of cubic unit cell= a= ?
Molar mass of ammonium bromide = 98 g/mol
Formula used :
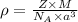
where,
 = density
= density
Z = number of atom in unit cell
M = atomic mass
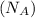 = Avogadro's number
= Avogadro's number
a = edge length of unit cell
On substituting all the given values , we will get the value of 'a'
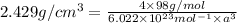
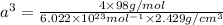
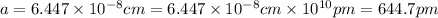
Ionic radius of bromide ion = r
To calculate the edge length, we use the relation between the radius and edge length for FCC lattice:
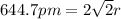
Putting values in above equation, we get:

Ionic radius of the bromide ion is 227.9 pm.