Question

seventy five percent of claims have a normal distribution with mean of 3000 and a variance of 1000000. the remaining 25% have a normal distribution with a mean of 4000 and variance of 1000000. determine the probability that a randomly selected claim exceeds 5000

Answer 1

P(x>5000) is approximately 0.05673 or 5.673%.

Explanation:

There are two different probabilities for the event that a randomly selected claim exceeds 5000; one is given for the probability that 75% of claims follows a normal distribution with parameters (3000, 1000000) and the other that 25% of claims follows a normal distribution with parameters (4000, 1000000).

Well, the probability of the event that a randomly selected claim exceeds 5000 is the sum of both probabilities, since they are mutually exclusive events, that is, one can occur independently from the other. That is, we can obtain some claims from one distribution or the other in a determined probability of 75% or 25%, respectively.

We already know that the standard deviation is the square root of the variance, so in both cases we have:

`\\ \sigma^2 = 1000000`

`\\ \sigma = √(1000000) = 1000`

In other words, a standard deviation of 1000, so we can rewrite the normal distributions as N(3000, 1000) for 75% of the claims and N(4000, 1000) for the rest 25% of the claims.

Then, if we rewrite the probabilities as follows:

Probability that a claim comes from distribution N1 = N(3000, 1000) is 75% or P(N1) = 0.75.

Probability that a claim comes from distribution N2 = N(4000, 1000) is 25% or P(N2) = 0.25.

Then, the probability of the event that a randomly selected claim exceeds 5000 can be mathematically expressed in the following way:

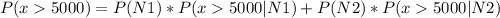`\\ P(x > 5000) = P(N1) * P(x>5000 | N1) + P(N2) * P(x>5000 | N2)` (1)

But we still need to determine the probabilities for:

`\\ P(x>5000 | N1)\;and\;P(x>5000 | N2)`

P(x>5000 | N1) or probability for values greater than 5000 for N(3000, 1000)

For this, we need to find the z-score for the raw value x = 5000 and then consult a cumulative standard normal table to find the probability that corresponds to this z-score.

`\\ z\;score = (x - \mu)/(\sigma)`

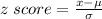
Where

`\\ \mu\;is\;the\;population\;mean`

`\\ \sigma\;is\;the\;population\;standard\;deviation`

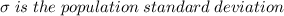
So

`\\ z = (5000 - 3000)/(1000)`

`\\ z = (5-3)*(1000)/(1000) = 2`

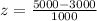
That is, the value of x = 5000 is two standard deviations above the mean (3000). A cumulative probability for P(z<2), using the cumulative standard normal table for z = 2 is 0.97725.

Thus

P(z<2) = 0.97725, and P(z>2) = 1 - P(z<2) = 1 - 0.97725 = 0.02275.

Because of the symmetry of the normal distribution, and remember that we are looking for values greater than 5000. This raw value represents a z-score = 2, that is why we are looking for P(z>2).

As a result, the probability for values greater than 5000 in N1 is about 0.02275 or

P(x>5000 | N1) = 0.02275

P(x>5000 | N2) or probability for values greater than 5000 for N(4000, 1000)

Following the former same steps, we have:

`\\ z = (5000 - 4000)/(1000)`

`\\ z = (5-4)*(1000)/(1000) = 1`

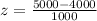
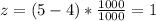
That is, the value of x = 5000 is one standard deviation above the mean (4000). A cumulative probability for P(z<1) using the cumulative standard normal table for z = 2 is 0.84134.

Thus

P(z<1) = 0.84134, and P(z>1) = 1 - P(z<1) = 1 - 0.84134 = 0.15866 (because of the symmetry of the normal distribution).

As a result, the probability for values greater than 5000 in N2 is about 0.15866 or

P(x>5000 | N2) = 0.15866

Then, we can determine the probability that a randomly selected claim exceeds 5000 using (1):

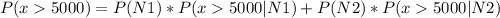`\\ P(x > 5000) = P(N1) * P(x>5000 | N1) + P(N2) * P(x>5000 | N2)` (1)

Since we have all the required information:

P(N1) = 0.75

P(N2) = 0.25

P(x>5000 | N1) = 0.02275

P(x>5000 | N2) = 0.15866

`\\ P(x > 5000) = 0.75 * 0.02275 + 0.25 * 0.15866`

`\\ P(x > 5000) \approx 0.05673`

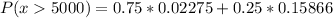
or P(x>5000) is approximately 0.05673 or 5.673%.

We can see in the graph below both probabilities for P(x>5000) assuming N1 and P(x>5000) assuming N2.