Question

There are 8 whole numbers in a set of numbers. The greatest number is 17, and the range is 9. The median and the mean are 12, but 12 is not in the data set. The modes are 9 and 14. What are the numbers?

Answer 1

`8,9,9,10,14,14,15,17`

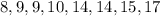
Explanation:

Let's order the whole numbers from least to greatest.

`a,b,c,d,e,f,g,h`.

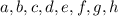We are given
`h=17`.

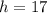We are also given the range is
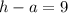`h-a=9` (biggest-smallest).

Since
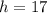`h=17` then we have that
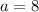`a=8` since
`17-8=9`.

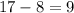The median is 12 means
`(d+e)/(2)=12`.

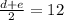If you multiply both sides by 2 you obtain
`d+e=24`.

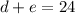We are also given
`(a+b+c+d+e+f+g+h)/(8)=12`.

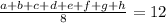Multiply both sides by 8:
`a+b+c+d+e+f+g+h=96`

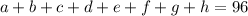
We know that
`d+e=24`,
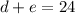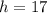`h=17`, and
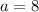`a=8`. This means this gives us the equation
`8+b+c+24+f+g+17=96`.

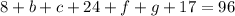We can combine like terms on the left hand side giving us:

`49+b+c+f+g=96`

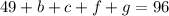
We can also subtract 49 on both sides:

`b+c+f+g=47`

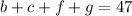
We are giving that
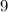`9` and
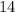`14` occur equal amount of times and that they occur the most of any whole number in our set.

This means they at least occur 2 times a piece. They couldn't occur 3 times a piece because that would force the median to be
`(9+14)/(2)=(23)/(2) \\eq 12`.

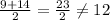So this is out list of numbers so far:

`8,9,9,d,e,14,14,17`.

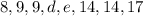Now we did have the equation
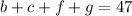`b+c+f+g=47` above.

We have now that
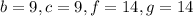`b=9,c=9,f=14,g=14` giving us the equation:

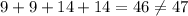`9+9+14+14=46 \\eq 47`. Let's assume there is something bigger than 14 occurs (less than 17 also since that is the maximum of the set). This forces 14 to be one of the two middles. This also means the other number is either 15 and 16. Let's pick 15 since we wanted 47 and that is 1 more than we got with other numbers we had.

So we are saying the new list:

`8,9,9,d,14,14,15,17`.

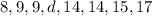Let's see if this works.

`b+c+f+g=47`

`9+9+14+15=18+29=47`

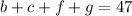
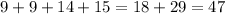
So this equation works.

Now what is the other middle. We were given that
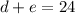`d+e=24` and we now have
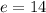`e=14` which means
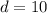`d=10` since
`10+14=24`.

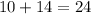So the data is
`8,9,9,10,14,14,15,17`.

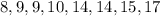Let's test it.

We have 8 whole numbers.

The greatest number is 17.

The range is 17-8=9.

The median is (10+14)/2=24/2=12.

The mean is (8+9+9+10+14+14+15+17)/8=(96)/8=12.

The modes are 9 and 14 since they occur the most over the other data.