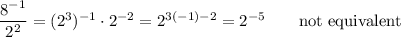Answer:
B, C, D
Explanation:
One of the rules of exponents is that an exponent in the numerator is equivalent to the opposite of the same exponent in the denominator. That means ...
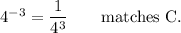
Another rule of exponents is that an exponent represents repeated multiplication. If a factor can be written using an exponent, the exponents are effectively multiplied.
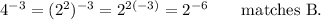
Of course, that repeated multiplication can be shown explicitly:
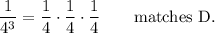
The equivalent expressions to 4^(-3) are B, C, D.
_____
Additional comment
The expression of G evaluates to ...