Question

A spelunker is surveying a cave. She follows a passage 140 m straight west, then 210 m in a direction 45 east of south, and then 280 m at 30 east of north. After a fourth unmeasured displacement, she nds herself back where she started. Determine the magnitude and direction of the fourth displacement.

Answer 1

301.96 m with direction of 10.4 degrees north of west

Step-by-step explanation:

Let i and j be the unit vector of east and north directions, respectively. So if she moving 140m straight west then her distance vector would be

`\vec{s_1} = -140\hat{i}`

When she walks 210 m in a direction 45 east of south, her displacement vector is:

`\vec{s_2} = 210sin45^0\hat{i} - 210cos45^0\hat{j}`

`\vec{s_2} = 210/√(2)\hat{i} - 210/√(2)\hat{j}`

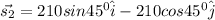
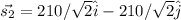
When she walks 280 m in a direction 30 east of north, her displacement vector is:

`\vec{s_3} = 280sin30^0\hat{i} + 280cos30^0\hat{j}`

`\vec{s_3} = 140\hat{i} + 140√(3)\hat{j}`

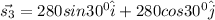
Then she walk another passage to be back to the origin

`\vec{s_1} + \vec{s_2} + \vec{s_3} + \vec{s_4} = 0\hat{i} + 0\hat{j}`

`140\hat{i} - 210/√(2)\hat{i} + 210/√(2)\hat{j} - 140\hat{i} - 140√(3)\hat{j} = x_4\hat{i} + y_4\hat{j}`

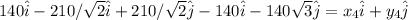
where x4 and y4 are the displacement she made in the east and north direction in her 4th displacement:

`x_4 = 140 - 210√(2) - 140 = -210√(2) \approx -297`

`y_4 = 210/√(2) - 140√(3) \approx 54.5`

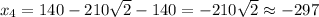
So her last displacement vector is

`\vec{s_4} = -297 \hat{i} + 54.5 \hat{j}`

This vector would have a displacement and direction of:

`s_4 = √(y_4^2 + x_4^2) = √(54.5^2 + -297^2) = √(2970.25 + 88209) = √(91179.25) = 301.96 m`

`tan\alpha= (y_4)/(x_4) = (54.5)/(297) = 0.18`

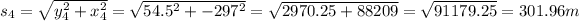
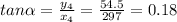
`\alpha = tan^(-1)0.18 = 0.18 rad \approx 10.4^o` north of west