Question

Boris invested his savings in two investment funds. The $12,000 that he invested in fund a returned a 6% profit the amount that he invested in fund b returned at 2% profit how much did he invest in Fund b if both funds together returned a 5%

Answer 1

$4000

Explanation:

Let B represent amount invested in account 'b'.

We have been given that an amount of $12,000 that Boris invested in fund a returned a 6% profit.

So the profit earned from fund 'a' would be
`12,000*(6)/(100)=12,000(0.06)`.

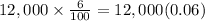We are also told that the amount that he invested in fund b returned at 2% profit. So the profit earned from fund 'b' would be
`B*(2)/(100)=B(0.02)=0.02B`.

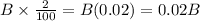Further, both funds together returned a 5%. We can represent this information as:

`(12,000+B)*(5)/(100)=0.05(12,000+B)`

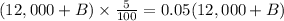
Now, we will equate profit earned from account 'a' and 'b' with profit earned from both accounts as:

`12,000(0.06)+0.02B=0.05(12,000+B)`

`720+0.02B=600+0.05B`

`600+0.05B=720+0.02B`

`600-600+0.05B=720-600+0.02B`

`0.05B=120+0.02B`

`0.05B-0.02B=120+0.02B-0.02B`

`0.03B=120`

`(0.03B)/(0.03)=(120)/(0.03)`

`B=4000`

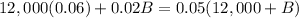
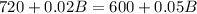
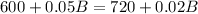
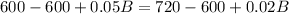
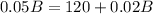
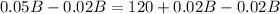
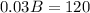
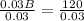
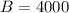
Therefore, Jason invested $4000 in fund 'b'.