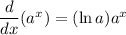Question

A population of bacteria can be modeled by the function f(t)= 400(0.98)t, where t is time in hours. What is the rate of change in the function?

Answer 1

C). decrease 2% per hour

Answer 2

`(d(f(t)))/(dt)=-8.08(0.98)^t`

Explanation:

We are given the following function:

`f(t)= 400(0.98)^t`

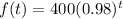
The function gives the population of bacteria in time, t where t is in hours.

We have to find the rate of change in function.

Rate of change =

`(d(f(t)))/(dt) = (d)/(dt)(400(0.98)^t)\\\\(d(f(t)))/(dt) = 400(\ln 0.98)(0.98)^t\\\\(d(f(t)))/(dt)=-8.08(0.98)^t`

is the required rate of change in function.

Differentiation property used:

`(d)/(dx)(a^x) = (\ln a)a^x`