Question

The ambient temperature is 85.0°F and the humidity of the surrounding air is reported to be 68.0%. Using the Clausius-Clapeyron equation and the boiling point of water as 100.0°C at 760 torr, calculate the vapor pressure (in torr) of water in the air. Use 40.7 kJ/mol as the ∆Hvap of water.

Answer 1

Answer: The vapor pressure of water in the air is 27.58 torr

Step-by-step explanation:

We are given:

Temperature of water in air = 85.0°F

Converting the temperature from degree Fahrenheit to degree Celsius is:

`^oF=(9)/(5)^oC+32`

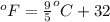
where,

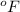`^oF` = temperature in Fahrenheit

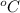`^oC` = temperature in centigrade

So,

`85.0^oF=(9)/(5)^oC+32\\\\T(^oC)=29.44^oC`

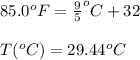
To calculate the final pressure, we use the Clausius-Clayperon equation, which is:

`\ln((P_2)/(P_1))=(\Delta H)/(R)[(1)/(T_1)-(1)/(T_2)]`

where,

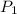`P_1` = initial pressure which is the pressure at normal boiling point = 760 torr

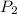`P_2` = final pressure = ?

`\Delta H_(vap)` = Enthalpy of vaporization = 40.7 kJ/mol = 40700 J/mol (Conversion factor: 1 kJ = 1000 J)

R = Gas constant = 8.314 J/mol K

`T_1` = initial temperature =
`100^oC=[100+273]K=373K`

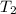`T_2` = final temperature =
`29.44^oC=[29.44+273]=302.44K`

Putting values in above equation, we get:

`\ln((P_2)/(760))=(40700J/mol)/(8.314J/mol.K)[(1)/(373)-(1)/(302.44)]\\\\P_2=35.72torr`

We are given:

68.0 % of water in the air

This means that 68 grams of water is present in the air

Mass of air = 100 - 68 = 32 g

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

• For water:

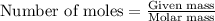
Molar mass of water = 18 g/mol

`\text{Moles of water}=(68g)/(18g/mol)=3.78mol`

• For air:

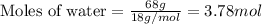
Average molar mass of air = 29 g/mol

`\text{Moles of air}=(32g)/(29g/mol)=1.103mol`

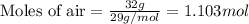
Mole fraction of a substance is given by:

`\chi_A=(n_A)/(n_A+n_B)`

`\chi_(water)=(n_(water))/(n_(water)+n_(air))\\\\\chi_(water)=(3.78)/(3.78+1.103)=0.774`

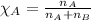
To calculate the mole fraction of substance, we use the equation given by Raoult's law, which is:

`p_(A)=p_T* \chi_(A)`

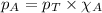
where,

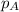`p_A` = vapor pressure of water = ?

`p_T` = total pressure = 35.72 torr

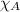`\chi_A` = mole fraction of water = 0.774

Putting values in above equation, we get:

`p_(water)=35.72* 0.772\\\\p_(water)=27.58torr`

Hence, the vapor pressure of water in the air is 27.58 torr