Question

A man-made satellite orbits the earth in a circular orbit that has a radius of 32000 km. The mass of the Earth is 5.97e 24 kg. What is the tangential speed of the satellite

Answer 1

3.53 x 10³ m/s

Step-by-step explanation:

When an object is undergoing a circular motion, the centripetal force (
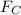`F_(C)`) acting on the body is equal to the vector sum of all forces acting on it. If the object is orbiting then the only force acting on it is the gravitational force (
`F_(G)`).

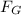In the case of the man-made satellite, the centripetal force (
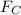`F_(C)`) is equal to the gravitational force (
`F_(G)`).

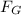i.e

`F_(C)` =
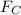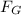`F_(G)` ---------------(i)

But;

`F_(C)` =
`(mv^2)/(r)`

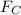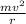
Where;

m = mass of the satellite.

v = tangential speed of the satellite.

r = radius of the path (orbit) of the satellite. = 32000km = 32000000m

Also as given by Newton's law of gravitational force between two bodies,

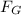`F_(G)` = G
`(m*M)/(r^2)`

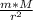
Where;

G = gravitational constant = 6.67 x 10⁻¹¹ Nm²/kg²

m = mass of satellite

M = mass of Earth = 5.97 x 10²⁴ kg

r = distance of separation between the earth and the satellite = radius of the orbit.

Substitute the values of
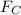`F_(C)` and
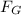`F_(G)` into equation(i) as follows;

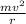`(mv^2)/(r)` = G
`(m*M)/(r^2)`

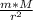
Divide through by m

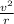`(v^2)/(r)` = G
`(M)/(r^2)`

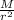
Multiply both sides by r

`v^(2)` = G
`(M)/(r)`

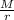
Find the square root of both sides;

`v` =
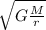`\sqrt{G(M)/(r) }` -------------------------------(ii)

Substitute the values of G = 6.67 x 10⁻¹¹ Nm²/kg², M = 5.97 x 10²⁴ kg and r = 32000000m into equation (ii) as follows;

`v` =
`\sqrt{(6.67*10^(-11) )(5.97*10^(24) )/(32000000) }`

`v` =
`\sqrt{(6.67*10^(-11) )(5.97*10^(24) )/(3.2*10^7) }`

`v` =
`\sqrt{(6.67*10^(-11) )({1.87*10^(17) }) }`

`v` =
`\sqrt{(12.47*10^(6) ) }`

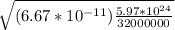
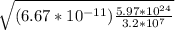
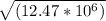
`v` = 3.53 x 10³ m/s

Therefore, the tangential speed of the satellite is 3.53 x 10³ m/s

Answer 2

= 3521m/s

The tangential speed is approximately 3500 m/s.

Step-by-step explanation:

F = m * v² ÷ r

Fg = (G * M * m) ÷ r²

(m v²) / r = (G * M * m) / r²

v² = (G * M) / r

v = √( G * M ÷ r)

G * M = 6.67 * 10⁻¹¹ * 5.97 * 10²⁴ = 3.98199 * 10¹⁴

r = 32000km = 32 * 10⁶ meters

G * M / r = 3.98199 * 10¹⁴ ÷ 32 * 10⁶

v = √1.24 * 10⁷

v = 3521.36m/s

The tangential speed is approximately 3500 m/s.