Question

Write a direct variation equation that relates x-miles and y- kilometers.

I mile is equal to 1.61 kilometers

Answer 1

The direct variation equation relating x miles and y kilometers is
`\( y = 1.61x \).`

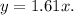
Step-by-step explanation:

In this context, the relationship between miles and kilometers is established by the conversion factor 1 mile = 1.61 kilometers. To express this relationship as a direct variation equation, we set up the formula
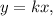`\( y = kx \),` where
`\( y \)` represents the dependent variable (kilometers),
`\( x \)` is the independent variable (miles), and
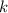`\( k \)` is the constant of variation. Since 1 mile is equivalent to 1.61 kilometers, the constant of variation
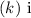`(\( k \)) i`s 1.61. Therefore, the direct variation equation is
`\( y = 1.61x \).`

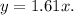
This equation is based on the principle that as the number of miles (\( x \)) increases or decreases, the corresponding number of kilometers (\( y \)) will vary proportionally with a constant rate of 1.61. This mathematical representation allows for a straightforward conversion between miles and kilometers. For example, if
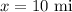`\( x = 10 \) mi`les, then
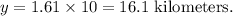`\( y = 1.61 * 10 = 16.1 \) kilometers.` The equation provides a simple and effective way to convert distances between the two units.

Understanding and utilizing direct variation equations are essential in various scientific and engineering applications where conversions between different units are frequent. In this case, the direct variation equation
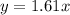`\( y = 1.61x \)` serves as a reliable tool for converting distances from miles to kilometers and vice versa, streamlining calculations and ensuring accuracy in unit conversions.

Answer 2

`y=1.60934x`

Step-by-step explanation:

If x is directly proportional to y, then

`y\propto x`

`y=kx`

where, k is constant of proportionality.

We know that,

1 miles = 1.60934 km

It is given that x-miles and y- kilometers. Constant of proportionality is 1.60934.

`y=1.60934x`

Hence, the required equation is
`y=1.60934x`.