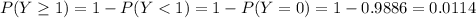Question

The automatic opening device of a military cargo parachute has been designed to open when the parachute is 185 m above the ground. Suppose opening altitude actually has a normal distribution with mean value 185 and standard deviation 30 m. Equipment damage will occur if the parachute opens at an altitude of less than 100 m. What is the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes? (Round your answer to four decimal places.)

Answer 1

`P(X<100)=P((X-\mu)/(\sigma)<(100-\mu)/(\sigma))=P(Z<(100-185)/(30))=P(Z<-2.833)`

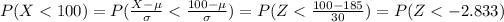
And we can find this probability using the normal standard table or excel:

`P(Z<-2.833)=0.0023`

`P(Y \geq 1)`

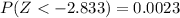
And we can use the complement rule like this:

`P(Y \geq 1)=1-P(Y<1) = 1-P(Y=0)`

`P(Y=0)=(5C0)(0.0023)^0 (1-0.0023)^(5-0)=0.9886`

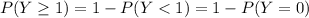
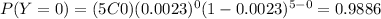
And if we replace we got:

`P(Y \geq 1)=1-P(Y<1) = 1-P(Y=0)=1-0.9886=0.0114`

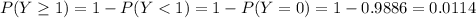
Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean". The letter
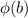`\phi(b)` is used to denote the cumulative area for a b quantile on the normal standard distribution, or in other words:
`\phi(b)=P(z<b)`

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Solution to the problem

Let X the random variable that represent the opening altitude of a population, and for this case we know the distribution for X is given by:

`X \sim N(185,30)`

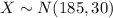
Where
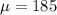`\mu=185` and
`\sigma=30`

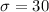
We are interested on this probability

`P(X<100)`

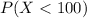
Since this represent the probability that one opening device fails

And the best way to solve this problem is using the normal standard distribution and the z score given by:

`z=(x-\mu)/(\sigma)`

If we apply this formula to our probability we got this:

`P(X<100)=P((X-\mu)/(\sigma)<(100-\mu)/(\sigma))=P(Z<(100-185)/(30))=P(Z<-2.833)`

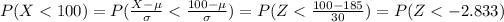
And we can find this probability using the normal standard table or excel:

`P(Z<-2.833)=0.0023`

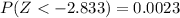
Let Y the random variable of interest "number of equipments with damage", on this case we now that:

`Y \sim Binom(n=5, p=0.0023)`

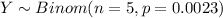
The probability mass function for the Binomial distribution is given as:

`P(Y)=(nCy)(p)^y (1-p)^(n-y)`

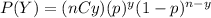
Where (nCx) means combinatory and it's given by this formula:

`nCy=(n!)/((n-y)! y!)`

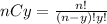
And we want to find this probability:

`P(Y \geq 1)`

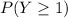
And we can use the complement rule like this:

`P(Y \geq 1)=1-P(Y<1) = 1-P(Y=0)`

`P(Y=0)=(5C0)(0.0023)^0 (1-0.0023)^(5-0)=0.9886`

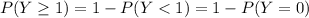
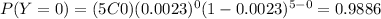
And if we replace we got:

`P(Y \geq 1)=1-P(Y<1) = 1-P(Y=0)=1-0.9886=0.0114`