Question

Identify the property that justifies the following statement:

If <1≈ <2, then <2≈<1.

Answer 1

Symmetric property of congruence.

Solution:

Given statement:

If ∠1 ≅ ∠2, then ∠2 ≅ ∠1.

To identify the property used in the above statement:

Let us first know some property of congruence:

Reflexive property:

The geometric figure is congruent to itself.

That is
`\overline{A B} \cong \overline{A B} \text { or } \angle B \cong \angle B`.

Symmetric property of congruence:

If the geometric figure A is congruent to figure B, then figure B is also congruent to figure A.

That is
`\overline{A B} \cong \overline{C D}, \text { then } \overline{C D} \cong \overline{A B}`.

Transitive property of congruence:

If figure A is congruent to figure B and figure B is congruent to figure C, then figure A is congruent to figure C.

That is
`\angle A\cong \angle B, \ \angle B\cong \angle C \ \text{then} \ \angle A\cong \angle C`

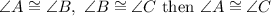
From the above properties, it is clear that,

If ∠1 ≅ ∠2 then ∠2 ≅ ∠1 is symmetric property of congruence.