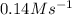Answer : The rate for a reaction will be
Explanation :
The balanced equations will be:
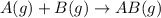
In this reaction,
 and
and
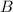 are the reactants.
are the reactants.
The rate law expression for the reaction is:
![\text{Rate}=k[A]^2[B]^1](https://img.qammunity.org/2021/formulas/chemistry/college/6nlujg8ikq36jd0hynfdzcwu8dw18ftgj8.png)
or,
![\text{Rate}=k[A]^2[B]](https://img.qammunity.org/2021/formulas/chemistry/college/6y33ra07okjrsklirgvu5i75giz97jb80x.png)
Now, calculating the value of 'k' by using any expression.
![\text{Rate}=k[A]^2[B]](https://img.qammunity.org/2021/formulas/chemistry/college/6y33ra07okjrsklirgvu5i75giz97jb80x.png)
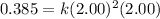
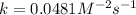
Now we have to calculate the initial rate for a reaction that starts with 1.48 M of reagent A and 1.32 M of reagents B.
![\text{Rate}=k[A]^2[B]^0[C]^1](https://img.qammunity.org/2021/formulas/chemistry/college/x30ozqm7nmwiba4egze0y7yzlgc403edz0.png)
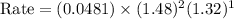
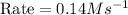
Therefore, the rate for a reaction will be