Question

The decline of salmon fisheries along the Columbia River in Oregon has caused great concern among commercial and recreational fishermen. The paper 'Feeding of Predaceous Fishes on Out-Migrating Juvenile Salmonids in John Day Reservoir, Columbia River' gave the accompanying data on y = maximum size of salmonids consumed by a northern squaw fish (the most abundant salmonid predator) and x = squawfish length, both in mm. Here is the computer software printout of the summary:

Coefficients:
Estimate Std. Error t value Pr(> |t|)
(Intercept) -89.010 16.702 -5.329 0.000
Length 0.740 0.047 15.678 0.000

Using this information, compute a 95% confidence interval for the slope.

Answer 1

The estimation for the slope on this case is
`\hat m = 0.740`

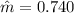
And the associated standard error is
`SE_(m)= 0.047`

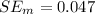
For the critical value we need to find the degrees of freedom given by:

Since we don't have the sample size we can assume it large enough to consider the normal approximation to the t distribution and on this case the critical value for 95% of confidence would be
`t_(\alpha/2) =1.96`

`0.740 -1.96*0.047= 0.648`

`0.740 +1.96*0.047= 0.832`

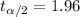
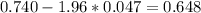
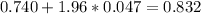
The confidence interval would be between (0.648, 0.832)

Explanation:

We are assuming that the estimation was using the least squares method

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

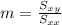
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

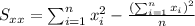
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(720)/(12)=60`

`\bar y= (\sum y_i)/(n)=(324)/(12)=27`

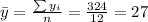
And we can find the intercept using this:

`b=\bar y -m \bar x`

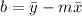
The confidence interval for this case is given by this formula:

`\hat m \pm t SE_(m)`

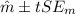
The estimation for the slope on this case is
`\hat m = 0.740`

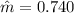
And the associated standard error is
`SE_(m)= 0.047`

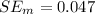
For the critical value we need to find the degrees of freedom given by:

Since we don't have the sample size we can assume it large enough to consider the normal approximation to the t distribution and on this case the critical value for 95% of confidence would be
`t_(\alpha/2) =1.96`

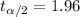
And replacing we got:

`0.740 -1.96*0.047= 0.648`

`0.740 +1.96*0.047= 0.832`

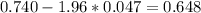
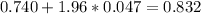
The confidence interval would be between (0.648, 0.832)