Question

A plane is missing, and is assumed to have an equalchance of being in one of three regions. If the plane is actually down in regioni, let 1−αibe the probability that the plane is found in a search of that region.What is the conditional probability that the plane is in:________.a. region 1, given that the search of region 1 was unsuccessful?b. region 2, given that the search of region 1 was unsuccessful?c. region 3, given that the search of region 1 was unsuccessful?

Answer 1

We can solve this problem using the Bayes' theorem.

Explanation:

Bayes' Theorem is used in calculating the probability of an event given a known fact.

E.g Probability of an event A, P(A) occurs given an event B, P(B) is given by

P(A|B) =
`(P(B|A)P(A))/(P(B))` =
`(P(B|A)P(A))/(P(B|A)P(A) + P(B|a)P(a))`

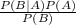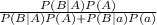
where

P(B|A) is probability of event B given event A

P(B|a) is probability of event B not given event A

and P(A), P(B), and P(a) are the probabilities of events A,B, and not event A respectively.

For this problem,

Let Probability of the plane in region 1, 2, and 3 be P(1), P(2) and P(3) respectively.

Let probability of successful search be P(F) and probability of unsuccessful search be P(U) which can be applied to any of the three regions.

From the question we know

P(1) = P(2) = P(3) = 1/3

and P(F₁|1) = 1 -
`\alpha`₁

Then P(U₁|1) = 1 - (1 -
`\alpha`₁) =
`\alpha`₁

Since for the three options it is given the plane is in region 1, hence P(1) = 1

(a.) Probability that the plane is in region 1 given an unsuccessful region 1 search = P(1|U₁)

If the plane is in regions 2 or 3, it can't be found in region 1

So, P(U₁|2) = P(U₁|3) = 1

Also, P(2) and P(3) = 1

P(1|U₁) =
`(P(U1|1)P(1))/(P(U1|1)P(1) + P(U1|2)P(2) + (P(U1|3)P(3))` =
`(\alpha 1)/(\alpha1 + 2 )`

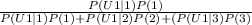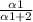
(b.) Probability that the plane is in region 2 given an unsuccessful search in region 1 = P(2|U₁)

P(2|U₁) =
`(P(U1|2)P(2))/(P(U1|1)P(1) + P(U1|2)P(2) + (P(U1|3)P(3))` =
`(1)/(\alpha1 + 2 )`

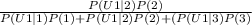(c.) Probability that the plane is in region 3 given an unsuccessful search in region 1 = P(3|U₁)

P(3|U₁) =
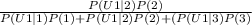`(P(U1|2)P(2))/(P(U1|1)P(1) + P(U1|2)P(2) + (P(U1|3)P(3))` =
`(1)/(\alpha1 + 2 )`