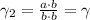Question

Orthogonalizing vectors. Suppose that a and b are any n-vectors. Show that we can always find a scalar γ so that (a − γb) ⊥ b, and that γ is unique if b 6= 0. (Give a formula for the scalar γ.) Roughly speaking, we can always subtract a multiple of a vector from another one, so that the result is orthogonal to the original vector. This is called orthogonalization, and is a basic idea used in the Gram-Schmidt algorithm.

Answer 1

`\\ \gamma= (a\cdot b)/(b\cdot b)`

Explanation:

The question to be solved is the following :

Suppose that a and b are any n-vectors. Show that we can always find a scalar γ so that (a − γb) ⊥ b, and that γ is unique if
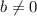`b \\eq 0`. Recall that given two vectors a,b a⊥ b if and only if
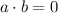`a\cdot b =0` where
`\cdot` is the dot product defined in
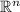`\mathbb{R}^n`. Suposse that
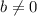`b\\eq 0`. We want to find γ such that
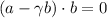`(a-\gamma b)\cdot b=0`. Given that the dot product can be distributed and that it is linear, the following equation is obtained

`(a-\gamma b)\cdot b = 0 = a\cdot b - (\gamma b)\cdot b= a\cdot b - \gamma b\cdot b`

Recall that
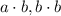`a\cdot b, b\cdot b` are both real numbers, so by solving the value of γ, we get that

`\gamma= (a\cdot b)/(b\cdot b)`

By construction, this γ is unique if
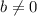`b\\eq 0`, since if there was a
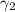`\gamma_2` such that
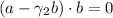`(a-\gamma_2b)\cdot b = 0`, then

`\gamma_2 = (a\cdot b)/(b\cdot b)= \gamma`