Question

The height in feet of a bottle rocket in given by h(t)=160t-16t^2 where t is the time in seconds. How long will it take for the rocket to return to ground ? What is the height after 2 secs? HELP ME PLEASE!!!!!!!!! Please show workkkkkk!!!!

Answer 1

a) 10 sec

b) 256 feet

Explanation:

a)

The height of the rocket above the ground at time t is described by the second-order equation

`h(t)=160t-16t^2` (1)

where:

t is the time, in seconds

h(t) is the height, in feet

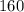`160` represents the initial vertical velocity of the rocket

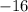`-16` represents the acceleration due to gravity (downward)

The rocket will return to the ground when the height is zero, so when

`h(t)=0`

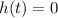
Substituting into eq(1) and solving for t, we find:

`0=160t-16t^2\\0=16t(10-t)=0`

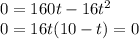
which has two solutions:

t = 0 (initial instant, so when the rocket starts its motion)

t = 10 s --> this is the time at which the rocket returns to the ground

b)

The height of the rocket is given by

`h(t)=160t-16t^2`

t is the time, in seconds

h(t) is the height, in feet

Here we want to find the height of the rocket after 2 seconds: to do that, we just need to substitute

t = 2 sec

into the equation of the height.

By doing so, we find:

`h(2)=160\cdot 2 -16(2)^2=256 ft`

Therefore, the height of the rocket after 2 seconds is 256 feet.