Question

At a certain instant, particles and have position vectors and velocities given by: Matlab/Mathematica input:

rP = [2,-5]
rQ = [-3,-6]
vP = [-7,-8]
vQ = [-2,-8]
What is the rate of change of the distance between points and ?

Answer 1

• 7m/s

Step-by-step explanation:

The vectors are:

• Positions (in meter)

Particle P

`\vec r_P=2\hat i-5\hat j`

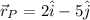
Particle Q

`\vec r_Q=-3\hat i-6\hat j`

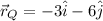
• Velocities (in meter per second)

Particle P

`\vec v_P=-7\hat i-8\hat j`

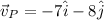
Particle Q

`\vec v_Q=-2\hat i-8\hat j`

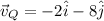
The rate of change of the relative positions of point P and Q is the relative velocity of one respect to the other.

The relative velocity of Q respect to P, in meter per second, is:

`\vec v_Q-\vec v_P=-2\hat i-8\hat j-(-7\hat i-8\hat j)\\\\\vec v_Q-\vec v_P=7\hat i`

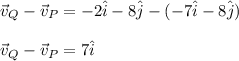
And the rate of change of the distance between points P and Q is the magnitude of the vector, which is 7m/s.