Question

Select the correct answer.
Rewrite the following equation as a function of x.

Answer 1

b

Explanation:

Answer 2

Option B:

`${f(x)}=9280-20x`

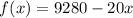
Solution:

`$(1)/(16) x+(1)/(320) y-29=0`

`$(1)/(16) x+(1)/(320) y-(29)/(1) =0`

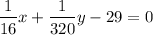
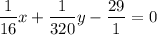
Take LCM of the denominators and Make the denominators same.

LCM of 16, 320, 1 = 320

`$(1*20)/(16*20) x+(1)/(320) y-(29* 320)/(1* 320) =0`

`$(20)/(320) x+(1)/(320) y-(9280)/(320) =0`

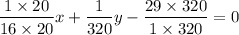
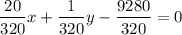
All the denominators are same, so you can write in one fraction.

`$(20x+y-9280)/(320)=0`

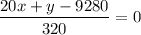
Do cross multiplication.

`${20x+y-9280}=0* 320`

`${20x+y-9280}=0`

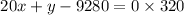
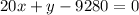
Add 9280 on both sides of the equation.

`${20x+y}=9280`

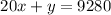
Subtract 20x on both sides of the equation.

`${y}=9280-20x`

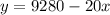
Let y = f(x).

`${f(x)}=9280-20x`

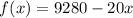
Hence Option B is the correct answer.