Question

Measurements indicate that boat A has twice the kinetic energy of boat B of the same mass. How fast is boat A traveling if boat B is moving at 34 ​knots? 1 knotequals1 nautical mile per hour​ [nmi/h]; 1 nautical mile ​[nmi]equals​6,076 feet​ [ft].

Answer 1

The speed of the boat-A is 47.84 knots.

Step-by-step explanation:

Mass of boat-A = m

Mass of boat-B = m

Kinetic energy if the boat-A = E

Kinetic energy if the boat-B = E'

Velocity of boat-A = v = ?

Velocity of boat-B = v'= 34 knots = 34 nautical miles /hour

1 knot = 1 nautical mile per hour

1 nautical mile ​= ​6,076 feet​

34 nautical miles /hour = 34 nautical miles /hour × 6,076 ft/miles = 205,564 ft/hour

Kinetic energy of boat-A is given by :

`E=(1)/(2)mv^2`

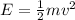
Kinetic energy of boat-A is given by :

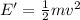`E'=(1)/(2)mv^2`..[1]

Kinetic energy of boat-B is given by :

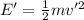`E'=(1)/(2)mv'^2`..[2]

E= 2E' (given)

[1] ÷ [2]

`(E)/(E')=((1)/(2)mv^2)/((1)/(2)mv'^2)`

`(2E')/(E')=(v^2)/(v'^2)`

`2* v'^2=v^2`

`2 * (205,564 ft/hour)^2=v^2`

`8.4513* 10^(10) ft^2/hour^2=v'^2`

`v'=290,711.4 ft/hour=(290,711.4)/(6,076) nautical mile/hour`

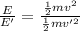
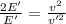
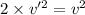
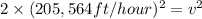
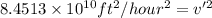
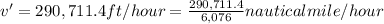
v' = 47.84 knots

The speed of the boat-A is 47.84 knots.