Question

A solid nonconducting sphere of radius R has a charge Q uniformly distributed throughout its volume. A Gaussian surface of radius r with r < R is used to calculate the magnitude of the electric field E at a distance r from the

center of the sphere. Which of the following equations results
from a correct application of Gauss’s law for this situation? And Why?

1. E (4 p r^2) = (Q r^3)/( epsilon sub0 * R3)
2. E(4pr^2)= (Q 3r^3)/ (epsilon sub0 * 4 p R)
3. E (4 p r^2) = (Q) / (epsilon sub0)

Answer 1

1. E x 4πr² = ( Q x r³) / ( R³ x ε₀ )

Step-by-step explanation:

According to the problem, Q is the charge on the non conducting sphere of radius R. Let ρ be the volume charge density of the non conducting sphere.

As shown in the figure, let r be the radius of the sphere inside the bigger non conducting sphere. Hence, the charge on the sphere of radius r is :

Q₁ = ∫ ρ dV

Here dV is the volume element of sphere of radius r.

Q₁ = ρ x 4π x ∫ r² dr

The limit of integration is from 0 to r as r is less than R.

Q₁ = (4π x ρ x r³ )/3

But volume charge density, ρ =
`(3Q)/(4\pi R^(3) )`

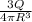
So,
`Q_(1) = (Qr^(3) )/(R^(3) )`

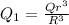
Applying Gauss law of electrostatics ;

∫ E ds = Q₁/ε₀

Here E is electric field inside the sphere and ds is surface element of sphere of radius r.

Substitute the value of Q₁ in the above equation. Hence,

E x 4πr² = ( Q x r³) / ( R³ x ε₀ )