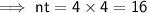Answer:
1.75% and 16 times
Explanation:
Compound interest formula:
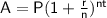
where:
- A = final amount
- P = initial principal balance
- r = annual interest rate (in decimal form)
- n = number of times interest applied per time period
- t = number of time periods
Given:
- P = $600
- r = 7% = 0.07
- n = 4
- t = 4
Substituting given values into the formula:
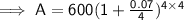
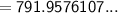
Equivalent interest rate:
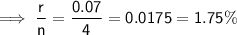
Number of times compounded: