Answer:
The value of stress in the rod is 220.9 MPa
Step-by-step explanation:
As the data is not complete, a similar question is found online and the missing data is used from that question. Similar question is attached herewith.
From the given data
The allowed total strain is given as
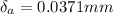
The length of the rod is missing in this data which in the additional data is l=290 mm
The Modulus of Elasticity is given as E=210 GPa
The coefficient of thermal expansion is given as α= 10 ×10⁻⁶ mm / mm⋅°C.
The initial temperature is room temperature which is given as T1=22C
The final temperature is given as T2=140 C
The strain due to stress is given as
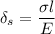

Now the thermal strain is given as
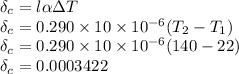
So now the equation of the allowed strain is given as
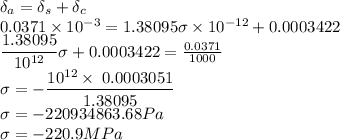
The negative sign indicate that the stress is compressive.
The value of stress in the rod is 220.9 MPa