Answer:
0.17
 0.096
0.096
Explanation:
We are given that Researchers are interested in determining whether more men than women prefer Coca Cola to Pepsi.
For this, In a random sample of 300 men, 65% prefer Coca Cola, whereas in a random sample of 400 women, 48% prefer Coca Cola.
The pivotal quantity for confidence interval is given by;
P.Q. =
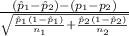 ~ N(0,1)
~ N(0,1)
where,
 = 0.65
= 0.65
 = 0.48
= 0.48
 = 300
= 300
 = 400
= 400
So, 99% confidence interval for the difference between the percentages of men and women who prefer Coca Cola over Pepsi is given by;
P(-2.5758 < N(0,1) < 2.5758) = 0.99 {At 1% significance level, the z table
gives value of 2.5758}
P(-2.5758 <
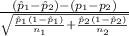 < 2.5758) = 0.99
< 2.5758) = 0.99
P(-2.5758 *
 <
<
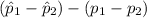 < 2.5758 *
< 2.5758 *
 ) = 0.99
) = 0.99
P(
 - 2.5758 *
- 2.5758 *
 <
<
 <
<
 + 2.5758 *
+ 2.5758 *
 ) = 0.99
) = 0.99
So, 99% confidence interval for
 =
=
[
 - 2.5758 *
- 2.5758 *
 ,
,
 + 2.5758 *
+ 2.5758 *
 ]
]
= [ (0.65 - 0.48) - 2.5758 *
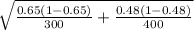 , (0.65 - 0.48) + 2.5758 *
, (0.65 - 0.48) + 2.5758 *
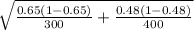 ]
]
= [ 0.17 - 2.5758 *
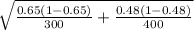 , 0.17 + 2.5758 *
, 0.17 + 2.5758 *
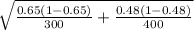 ]
]
= [ 0.17 - 0.096 , 0.17 + 0.096 ] = [0.17
 0.096]
0.096]
Therefore, 99% confidence interval for the difference between the percentages of men and women who prefer Coca Cola over Pepsi is 0.17 ± 0.096 .